Вы наверняка слышали о теории хаоса и об «эффекте бабочки» — когда один взмах её крыльев вызывает ураган в другом конце планеты . При этом все понимают, что такого не может быть. На Земле летают миллиарды этих насекомых, и если бы даже триллионная часть их взмахов заканчивалась природными катаклизмами, то от человечества давным-давно ничего не осталось бы. Так откуда же взялось это популярное выражение? Дело в том, что мы его не совсем правильно воспринимаем. Эта идея весьма популярна у фантастов, описывающих путешествия во времени. Здесь и бесконечно плодящиеся альтернативные вселенные, где убивают Гитлера и спасают Кеннеди, и другие не менее оригинальные порождения творческого гения. Однако чтобы понять, как она возникла, придётся вернуться к самому началу эпохи компьютеров, в 60-е годы прошлого века, а также к истокам метеорологии.
Погода на Земле определяется потоками воздуха и воды. Практически всё, от лёгкого бриза до урагана, можно объяснить, рассматривая их течение. Однако предсказать поведение этих потоков трудно из-за крайней своеобразности гидроаэродинамики. Её уравнения трудны в применении, а решения, как правило, сложны и беспорядочны. До начала 20 века прогнозирование погоды было больше искусством, чем наукой, но в упомянутые шестидесятые в университетах начали появляться компьютеры, которые исследователи приспособили для решения своих уравнений. И сразу же они столкнулись с проблемой, которая впоследствии навсегда изменила и математику, и физику.
Если нужно смоделировать физическую систему, будь то погода над Занзибаром или ускоритель частиц, приходится решать дифференциальные уравнения — они показывают, как данная система меняется с течением времени. При этом в них всегда закладываются исходные условия. В принципе, это выглядит так — вы описываете, как ситуация выглядит изначально, а затем уравнения позволяют увидеть, во что это выльется.
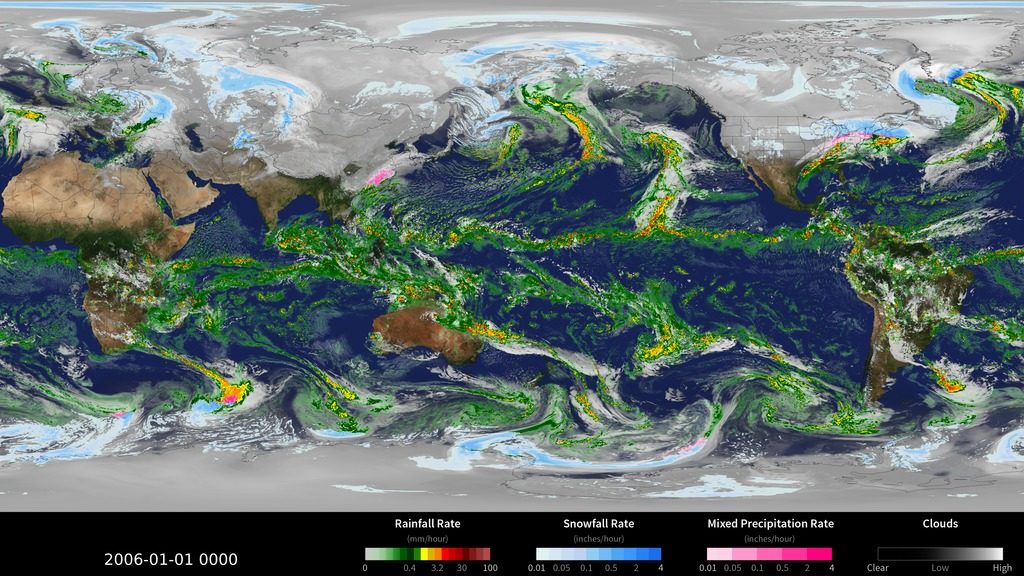
Одним из первых, кто использовал компьютер для прогнозирования погоды, был Эдвард Лоренц. В 1961 году, проводя симуляцию упрощённой погодной системы, он сделал необычное открытие. Одни и те же уравнения, имеющие одинаковые начальные условия, выдали два разных прогноза. Как такое могло произойти? Ведь по описанию это кажется невозможным, не правда ли? Присмотревшись внимательнее, Лоренц увидел, что два начальных параметра совпадали не полностью. В одном случае он, искренне считая, что это ничего не изменит, сократил число 0.506127 до 0.506. Как выяснилось, он серьёзно ошибался. Это было далеко не незаметное отличие — разночтения удваивались каждые четыре дня симулируемого времени, и через месяц изменили результаты настолько, что они перестали напоминать друг друга.
Учёный сделал совершенно правильный вывод, что даже крошечные изменения начальных условий могут привести к кардинально иному итогу. Лоренц рассказал об этом в лекции, которую назвал «Взмах крыльев бабочки в Бразилии вызывает торнадо в Техасе?». Однако он был осторожен в своём выступлении и не говорил ничего вроде «все торнадо вызваны бабочками» или «все бабочки генерируют торнадо». Его посыл заключался в том, что кажущиеся малозначительными события могут иметь масштабные последствия. То есть если вы представите себе две планеты, которые идентичны во всём, кроме одной бабочки, то теоретически возможно, что на одной из них случится торнадо, а на другой — нет.
Теперь вы знаете, как появился «эффект бабочки», и какой смысл в него вкладывал автор. В лекции Лоренца было ещё немало достойных внимания выводов. Вроде того, что мы не можем знать, какой именно взмах крыльев, если таковой был, мог изменить погоду. Он утверждал, что не имея бесконечной вычислительной мощности, мы не можем проследить все микроскопические источники воздействий. Также он предположил, что с той же вероятностью, с какой бабочка может вызвать торнадо, она способна и предотвратить его.
Открытие Лоренца со временем привело к появлению теории хаоса. Она применяется в системах, чрезвычайно чувствительных к начальным условиям, вроде той же погоды. Там, где небольшие изменения в прошлом имеют огромные последствия в будущем. Многие учёные вообще считают эту теорию новой областью математики — потому что она, как кажется, может найти применение повсюду. Гравитационное взаимодействие колец Сатурна, раскачивание двойного маятника, переворот магнитного поля Земли, даже некоторые макроэкономические процессы… Самое потрясающее во всём этом то, что подобные системы, несмотря на хаотичность своей природы, действительно имеют много общего. По всей видимости, внутри хаоса существуют некая упорядоченность и универсальные правила поведения. Например, если представить их свойства графически, то очень часто можно увидеть фракталы — удивительные, бесконечно повторяющиеся узоры. Но это тема уже для отдельного разговора.
Анимация охватывает период с 1 марта 2007 г. по 16 июня 2007 г.
Что всё вышесказанное означает для метеорологии? Она за последние десятилетия действительно стала гораздо точнее в предсказаниях благодаря заметному улучшению качества начальных данных, поставляемых спутниками, метеостанциями и другими средствами наблюдения. Более мощные компьютеры, гораздо более совершенные алгоритмы и модели — всё это позволяет лучше видеть вероятное развитие погодных процессов. Естественно, не последнюю роль играет и понимание теории хаоса. Однако всё то, что находится за пределами двух-трёх дней, до сих пор, по большому счёту, скрыто от нас «туманом войны». Точно так же, как в квантовой механике, законы физики накладывают строгие ограничения на нашу способность прогнозировать. Теория хаоса окружает нас со всех сторон, на многих уровнях бытия. Это и потоки воздуха, и ход истории, и поведение фондовых рынков. Попытаться понять их — задача в высшей степени интересная и благородная.








